Question

F(x) = x3 + x2 + 1; interval [0, 4); 4 subintervals O 54 0 135 134 52

Answer 1

The lenght of the interval [0,4] is 4. To calculate the area under the curve we need to divide this interval in equal parts and calculate the area of the rectangles with height given by the left end point of each subinterval.

In this case we have that each rectangle will have base given by:

`\Delta x=(b-a)/(4)=(4-0)/(4)=1`

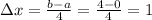
Then our subtinervals will be:

`\begin{gathered} \lbrack0,1\rbrack \\ \lbrack1,2\rbrack \\ \lbrack2,3\rbrack \\ \lbrack3,4\rbrack \end{gathered}`

Now, the area of the will be:

`\begin{gathered} A=\Delta xf(0)+\Delta xf(1)+\Delta xf(2)+\Delta xf(3) \\ =1(0^3+0^2+1)+1(1^3+1^2+1)+1(2^3+2^2+1)+1(3^3+3^2+1) \\ =1(1)+1(3)+1(13)+1(37) \\ =1+3+13+37 \\ =54 \end{gathered}`

Therefore, the approximation of the area will be 54.