Question

f(x) = x3 – 10x2 + 31x – 30 Step 2 of 3: Use synthetic division to identify integer bounds of the real zeros. Find the least upper bound and the greatest lower bound guaranteed by the Upper and Lower Bounds of Zeros theorem.

Answer 1

`f(x)=x^3-10x^2+31x-30`

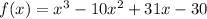
Test x = 2 and use it to find f(2) to and determine if (x-2) is factor of the polynomial f(x)

`\begin{gathered} f(2)=2^3-10(2^2)+31(2)-30 \\ =8-10(4)+62-30 \\ =8-40+62-30 \\ =0 \end{gathered}`

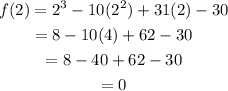
Since f(2) = 0, it means (x - 2) is a factor of the polynomial, let us show this with synthetic division

2 | 1 -10 31 -30

2 -16 30

1 -8 15 0

This shows that 2 is a zero.

Doing the same for 3 and 5, we have

3 | 1 -10 31 -30

3 -21 30

1 -7 10 0

Thus, 3 is also a zero.

For 5, we have,

5 | 1 -10 31 -30

5 -25 30

1 -5 6 0

Thus, 5 is also a zero.

The lower zeros is 2 while the upper zeros is 5