9 years
Step-by-step explanation
Step 1
set the equations.
let
x represents the lisa's age
y represents the twin bother's age
so
a)the product of the ages of Lisa and her twin bothers is 36
hence
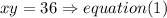
b)and the sum of their ages is 13
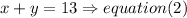
Step 2
solve the equations
a) isolate the y value in equation (2) then replace in eqaution (1)
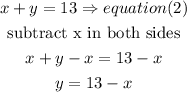
now , replace in eq(1)
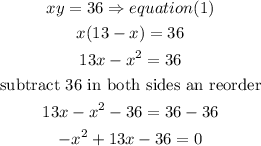
we need to solve this quadratic equation, let's use the quadratic formula
![\begin{gathered} \text{for ax}^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uxwb6k7jncf6l0uefu65f47j8vt5iuxgs2.png)
hence
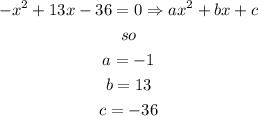
now, to find the solutino for x, let's replace in the formula
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(13)\pm\sqrt[]{13^2-4(-1)(-36)}}{2(-1)} \\ x=\frac{-(13)\pm\sqrt[]{169-144}}{-2} \\ x=\frac{-(13)\pm\sqrt[]{25}}{-2} \\ x=(-(13)\pm5)/(-2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/inho3xzubytl2yjp6l3ep5qfmpbia1q1yp.png)
we have the symbol

it means, there are two solutions, let's check

so,
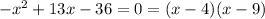
Step 3
let's solve the quadratic equation by factoring

so, the posibles values for Lisa´s age are
9 or 4
as we don't know who is older, the ages are 4 and 9
let's prove
a)the product of the ages of Lisa and her twin bothers is 36
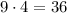
b)
and the sum of their ages is 13.
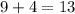
I hope this helps you
x