we have that
To find the sum of the first Sn terms of a geometric sequence use the formula
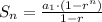
where
a1=120 -----> first term
n=8
Find out the common ratio r
we have
a1=120
a2=-80
a3=160/3
so
a3/a2=(160/3)/(-80)=-2/3
a2/a1=-80/120=-2/3
so
r=2/3
substitute given values in the formula
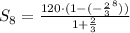
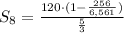
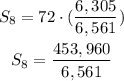
Simplify
S_8=50,440/729