Question

Find all the zeros of polynomial functionsf(x)=24x^4-2x^3-35x^2-4x+5

Answer 1

To find the zeros of a polynomial, we can graph the function given as follows:

From the graph, we have that the roots are:

• (-1, 0)

,

• (-1/2, 0)

,

• (1/3, 0) (We can express 1/3 as a periodic decimal as 0.33333...)

,

• (5/4, 0) (5/4 is equivalent to 1.25).

We have that the Fundamental Theorem of Algebra tells us that this fourth-degree polynomial must have 4 roots (including multiple and complex roots).

In this case, we have four different roots.

They are NOT multiple (repeated roots) or complex roots. We have four rational roots, and we can verify them from the graph. The roots are those ones where the function passes through the x-axis and when y = 0.

Therefore, these roots are x = -1, x = -1/2, x = 1/3, x = 5/4.

We can check this result if we substitute each of these values into the polynomial function, f(x):

`f\mleft(x\mright)=24x^4-2x^3-35x^2-4x+5`
`f(-1)=24\cdot(-1)^4-2\cdot(-1)^3-35\cdot(-1)^2-4\cdot(-1)+5=24+2-35+4+5=0_{}`

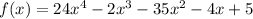
And we can do the same for the rest of the roots: x = -1/2, x = 1/3, x = 5/4, we will obtain zero for the function, f(x).