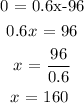Question

A vehicle factory manufactures cars. The unit cost C (the cost in dollars to make each car) depends on the number of cars made. If x cars are made, then theunit cost is given by the function C (x) = 0,3x2 -96x+14,848. How many cars must be made to minimize the unit cost?Do not round your answer

Answer 1

`160\text{ cars}`

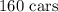
Step-by-step explanation:

Here, we want to get the number of cars to be made so as to minimize the unit cost

What we have to do here is to find the first derivative of the given cost function

Mathematically, we have that as:

`C^(\prime)(x)\text{ = 0.6x -96}`

To get the minimum x value, we simply set the first derivative to zero and solve for x

Mathematically, that would be:

`\begin{gathered} 0\text{ = 0.6x-96} \\ 0.6x\text{ = 96} \\ x\text{ = }(96)/(0.6) \\ x\text{ = 160 } \end{gathered}`