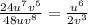Question

Apply all relevant properties of exponents to simplify the following expression.assume all variables are nonzero all exponents entered should be positive

Answer 1

`(24u^7v^5)/(48uv^8)=(u^6)/(2v^3)`

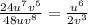
Solution

- The question asks us to simplify the following expression:

`(24u^7v^5)/(48uv^8)`

- In order to solve this, we need to know some laws of exponents to help us with the solution. The relevant laws of exponents for this question are given below:

`\begin{gathered} \text{Law 1:} \\ (a^b)/(a^c)=a^(b-c) \\ \\ \text{Law 2:} \\ \frac{abc}{\text{xya}}=(a)/(x)*(b)/(y)*(c)/(z) \\ \\ \text{Law 3:} \\ a^(-b)=(1)/(a^b) \end{gathered}`

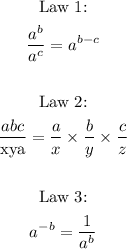
- Now that we have the laws of exponents we require, we can proceed to solve the question.

- This is done below:

`\begin{gathered} (24u^7v^5)/(48uv^8) \\ \\ \text{Apply Law 2:} \\ (24u^7v^5)/(48uv^8)=(24)/(48)*(u^7)/(u)*(v^5)/(v^8) \\ \\ \text{Apply Law 1 } \\ (24)/(48)*(u^7)/(u)*(v^5)/(v^8)=(24)/(24*2)* u^(7-1)* v^(5-8) \\ \\ =(1)/(2)* u^6* v^(-3) \\ \\ \therefore(24u^7v^5)/(48uv^8)=(1)/(2)* u^6* v^(-3) \\ \\ \text{But we are told to keep all exponents positive, thus, we should apply Law 3 to }v^(-3) \\ \\ (1)/(2)* u^6* v^(-3)=(1)/(2)* u^6*(1)/(v^3)=(u^6)/(2v^3) \\ \\ (24u^7v^5)/(48uv^8)=(u^6)/(2v^3) \end{gathered}`

Final Answer

`(24u^7v^5)/(48uv^8)=(u^6)/(2v^3)`