Question

Write the point slope form of the line satisfying the given conditions. Then use the point slope form of the equation to write the slope intercept form of the equation. Slope=7Passing through (-6,1)

Answer 1

Ok, so

The point slope form of the line is given by the following formula:

`(y-y_1)=m(x-x_1)`

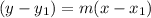
Where

`(x_1,y_1)`

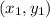
Is a point of the line, and m is the slope.

If we replace our values:

Slope = 7

Point = (-6, 1)

We obtain that the equation is:

`\begin{gathered} (y-1)=7(x-(-6)) \\ (y-1)=7(x+6) \end{gathered}`

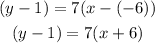
To find the slope intercept form of the equation, we distribute in the brackets:

`\begin{gathered} y-1=7x+42 \\ y=7x+43 \end{gathered}`

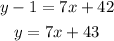
And the equation of our line in the slope intercept form will be:

y=7x+43