ANSWER:
Not real but imaginary solutions because the equations do not intersect
Explanation:
We have the following system of equations:
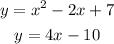
Graph each one through the graphing program and we have the following:
Both graphs do not intersect, therefore we can conclude that the answer in part a is correct, since the solution does not belong to the real numbers, but to the imaginary numbers.