Question

Show that tangent is an odd function.Use the figure in your proof.

Answer 1

We have to prove that the tangent is an odd function.

If the tangent is an odd function, the following condition should be satisfied:

`\tan(t)=-\tan(-t)`

From the figure we can see that the tangent can be expressed as:

We can start then from tan(t) and will try to arrive to -tan(-t):

`\begin{gathered} \tan(t)=(\sin(t))/(cos(t))=(y)/(x) \\ \tan(t)=(-(-y))/(x)=(-\sin(-t))/(\cos(-t)) \\ \tan(t)=-(\sin(-t))/(\cos(-t)) \\ \tan(t)=-\tan(-t) \end{gathered}`

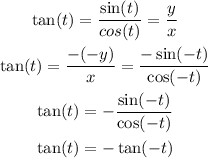
We have arrived to the condition for odd functions, so we have just proved that the tangent function is an odd function.