Question

I don’t know how to solve these problems or where to even start??

Answer 1

We'll solve question 1.

a)

Simplifying,

`(3+4i)+(1-2i)\rightarrow3+4i+1-2i\rightarrow4+2i`

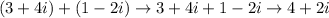
b)

Remember that we can express any complex number

`\alpha+\beta i`

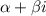
on the plane as

`(\alpha,\beta)`

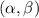
Thereby, our imaginary number 4 + 2i on the plane would look as following:

c)

Since we already have rectangular coordinates for our complex number, we can rewrite it in polar coordinates. Remember that to put any set of rectangular coordinates (x,y) on the polar plane, we use the following:

`\begin{gathered} r=\sqrt[]{x^2+y^2} \\ \theta=\tan ^(-1)((y)/(x)) \end{gathered}`

This way,

`r=\sqrt[]{4^2+2^2}\rightarrow r=\sqrt[]{20}\Rightarrow r=2\text{ }\sqrt[]{5}`
`\theta=\tan ^(-1)((2)/(4))\Rightarrow\theta=26.57`

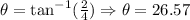
Therefore, our complex number in polar coordinates would be

`2\text{ }\sqrt[]{5}\text{ }\angle26.57`

d)

The plot would look as following: