Question

Consider the system of linear equations.y =3/4x+12y=4/3xPart AHow many solutions does the system have?A. no solutionB. exactly one solutionC. exactly two solutionsD. infinitely many solutionsPart BHow can you tell?A. The slopes of the equations are the same so the lines will not intersect.B. The slopes of the equations are different so the lines will intersect at one pointC. The slopes of the equations are different so the lines will intersect twiceD. The slopes of the equations are the same so the lines will both be the same line.

Answer 1

Given the system of equations:

`\begin{cases}y=(3)/(4)x+10 \\ y=(4)/(3)x\end{cases}`

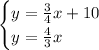
notice that both lines have different slopes(4/3 and 3/4) , therefore, they intersect in one point.

That point is the only solution of the system, therefore,we have the following:

Part A: The system has exactly one solution

Part B: the slopes of the equations are different, so the lines will intersect at one point