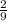SOLUTION
This is a probability question that has to do with the "without replacement" scenario, because every chocolate eaten leaves the box and never returns
The probability that both pieces are milk chocolate is calculated thus:
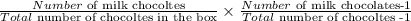
Number of milk chocolates = 5
NUmber of dark chocolates = 5
Total number of chocolates in the box = 5+5 =10
The probability that both pieces are milk chocolate is:
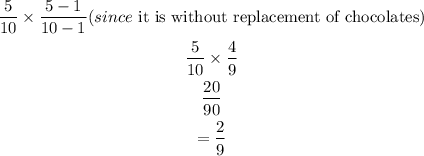
The probability that both pieces are milk chocolate is: