A triangle has sides of length 12 cm and 21 cm with an included angle of 56 degrees.Find the expression for the height to the 21 cm side (not an approximation).The height is ___…

Question

asked Jan 11, 2023 13.9k views

1 Answer

Rahul Tokase · Answer 1 · 2023-01-17T12:30:21+0000

Answer:

• Height= 21 sin56°

,

• The area of this triangle is approximately equal to 104 squared centimeters.

,

• The units are centimeter (for height) and squared centimeter (for the area)

Step-by-step explanation:

The sides lengths of the triangle are 12 cm and 21 cm respectively.

The included angle (angle between the two given sides) is 56 degrees.

The diagram representing this is attached below.

Using trigonometric ratios, the expression for the height to the 21 cm side is:

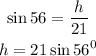
$\begin{gathered} \sin 56=(h)/(21) \\ h=21\sin 56^0 \end{gathered}$

We know that the area of a triangle is calculated using the formula:

$\begin{gathered} \text{Area}=(1)/(2)*\text{Base}* Height \\ =(1)/(2)*12*21\sin 56^0 \\ \approx104.46\operatorname{cm}^2 \end{gathered}$

• The area of this triangle is approximately equal to 104 squared centimeters.

,

• The units are centimeter (for height) and squared centimeter (for the area).