Question

The annual profits for a company are given in the following table, where x representsthe number of years since 1997, and y represents the profit in thousands of dollars.Write the linear regression equation that represents this set of data, rounding allcoefficients to the nearest tenth. Using this equation, find the projected profit (inthousands of dollars) for 2008, rounded to the nearest thousand dollars.

Answer 1

Explanation:

Answer 2

A Linear regression line has an equation in the form,

y= ax+b

where Y= Dependent variable

X= Independent variable

a= The intercept

b= The slope of the line.

So we are to get the summation of all the tables formulated.

`\begin{gathered} \sum ^{}_{}x=\text{ 15} \\ \sum ^{}_{}y=797 \\ \sum ^{}_{}xy=2464 \\ \sum ^{}_{}x^2=\text{ }55 \\ \sum ^{}_{}y^2=\text{ 119875} \end{gathered}`

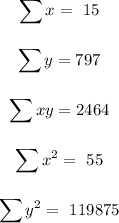
We are to solve for the mean of x, mean of y, a and b.

`\begin{gathered} \bar{x}=\text{ }\frac{\sum ^{}_{}x}{n} \\ \bar{y}=\text{ }\frac{\sum ^{}_{}y}{n} \\ a=\text{ }\frac{n\sum ^{}_{}xy-(\sum ^{}_{}x)(\sum ^{}_{}y)}{n\sum ^{}_{}x^2-(\sum ^{}_{}x)^2} \\ b=\text{ }\bar{y}-a\bar{x} \end{gathered}`
`\begin{gathered} where\text{ n=6} \\ \bar{x}=\text{ }(15)/(6)=2.5 \\ \bar{y}=\text{ }(797)/(6)=\text{ 132.8} \end{gathered}`
`\begin{gathered} a=(6(2464)-(15)(797))/(6(55)-(15)^2) \\ a=\text{ }(14784-11955)/(330-225) \\ a=\text{ }(2829)/(105) \\ a=\text{ 26.9} \end{gathered}`
`\begin{gathered} b=\bar{y}-\bar{ax} \\ b=\text{ }132.8-(26.9)(2.5) \\ b=\text{ 132.8- 67.25} \\ b=\text{ 65.55}\approx65.6 \end{gathered}`

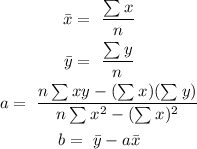
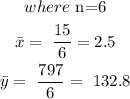
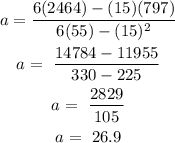
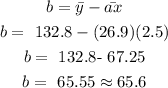
Hence the regression line equation is:

y=ax+b

y=26.9x+65.6

To find the projected profit of the year 2008, we would make use of the derived equation, y=26.9x+65.6

where x= 2008-1997= 11years,

y=?

Solving for y,

y= 26.9×11+65.6

y= 295.9+65.6

y= 361.15(thousand dollars) to the nearest thousand dollars

y= $361,000.

Hence the value for y= $361,000.