The volume of a basketball can be given as volume of a shpere below,
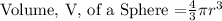
Let the volumes of the original and inflated basketball be given below respectively as,
![\begin{gathered} \text{Vol of original = V}_1 \\ \text{Vol of inflated basketball =V}_2=225\operatorname{cm}^3 \end{gathered}]()
To find the radius of the inflated basketball below,
![\begin{gathered} V_2=(4)/(3)\pi r^3=225\operatorname{cm}^3 \\ \text{Crossmultiply} \\ (4)/(3)\pi r^3=3*225=675 \\ 4\pi r^3=675 \\ r^3=(675)/(4\pi) \\ \text{Where }\pi=3.14 \\ r^3=(675)/(4*3.14)=53.742 \\ r=\sqrt[3]{53.742} \\ r=3.77\operatorname{cm} \end{gathered}]()
Radius r₂ of the inflated basketball is 3.77cm
Given the radius ratio of the original to the inflated basketball below as,
![\begin{gathered} Ratio\text{ of original to inflated baskteball=}(4)/(9) \\ \text{Where the radius of the inflated baskteball is 3.77} \\ To\text{ find the radius of the original basketball} \\ (4)/(9)=(r_1)/(r_2)=(r_1)/(3.77) \\ \text{Crossmultiply} \\ 4*3.77=r_1*9 \\ r_1=(4*3.77)/(9)=1.68\operatorname{cm} \\ r_1=1.68\operatorname{cm} \end{gathered}]()
To find the volume of the original basketball using the formula for the volume of a sphere,
![\begin{gathered} V_1=(4)/(3)\pi r^3=(4)/(3)*3.14*(1.68)^3=19.85\operatorname{cm}^3 \\ V_1=20\operatorname{cm}^3(nearest\text{ whole number)} \end{gathered}]()
The volume V₁ of the original basketball is 20cm³(nearest whole no)