Question

Addition and Scalar Multiplication of MatricesJun 06, 10:34:39 PMWatch help videoGiven the matrices A and B shown below, find 2B + } A.37-1-6lis[-91818.6B의127

Answer 1

We have two matrices, and we want to do an operation with them. When you multiply a matrix by a scalar, it is the same as multiplying each element of the matrix by this scalar, and when you sum two matrices, you add each corresponding element(for this, the matrices MUST be the same size).

We have the following matrices:

`A=\begin{bmatrix}-9{} & {18} & {3} \\ {18} & {6} & {-3}\end{bmatrix},B=\begin{bmatrix}{7} & {-1} & {-6} \\ {}12 & {7} & {-1}\end{bmatrix}`

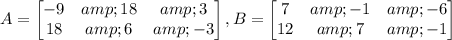
And we want to do the following operation.

`2B+(1)/(3)A`

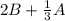
First, we'll multiply B by 2 and A by 1/3

`\begin{gathered} 2B=2\begin{bmatrix}{7} & {-1} & {-6} \\ {}12 & {7} & {-1}\end{bmatrix}=\begin{bmatrix}2*{7} & {2*-1} & {2*-6} \\ {}2*12 & {2*7} & {2*-1}\end{bmatrix} \\ =\begin{bmatrix}{14} & {-2} & {-12} \\ {}24 & {14} & {-2}\end{bmatrix} \end{gathered}`
`(1)/(3)A=\begin{bmatrix}-3 & {6} & {1} \\ {6} & {2} & {-1}\end{bmatrix}`

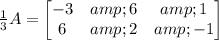
Now, we just add each element.

`\begin{gathered} 2B+(1)/(3)A=\begin{bmatrix}{14} & {-2} & {-12} \\ {}24 & {14} & {-2}\end{bmatrix}+\begin{bmatrix}-3 & {6} & {1} \\ {6} & {2} & {-1}\end{bmatrix} \\ =\begin{bmatrix}14+(-3) & (-2)+{6} & (-12)+{1} \\ {24+6} & {14+2} & (-2)+({-1)}\end{bmatrix}=\begin{bmatrix}11 & {4} & -{11} \\ {30} & {16} & {-3}\end{bmatrix} \end{gathered}`

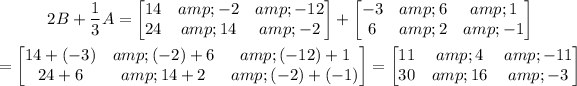
And this is our final answer:

`\begin{bmatrix}11 & {4} & -{11} \\ {30} & {16} & {-3}\end{bmatrix}`