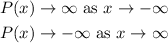Question

Identify the correct leading coefficient, degree and end behavior of P(x)=-2x^5+7x^4-5x^3-x^2+8x-1

Answer 1

• The degree of the polynomial = 5

,

• The leading coefficient of the polynomial = -2

,

• End Behavior: The graph rises to the left and falls to the right.

Explanation:

Given the polynomial:

`P\mleft(x\mright)=-2x^5+7x^4-5x^3-x^2+8x-1`

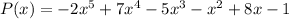
• The degree of the polynomial = 5 (,Odd,)

,

• The leading coefficient of the polynomial = -2 (,Negative,)

In order to determine the end behavior of P(x), we employ the use of the leading coefficient test.

By the leading coefficient test, when the degree is odd and the leading coefficient is negative, the graph rises to the left and falls to the right.

That is:

`\begin{gathered} P(x)\to\infty\text{ as }x\to-\infty \\ P(x)\to-\infty\text{ as }x\to\infty \end{gathered}`