Given two points
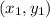
and
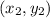
The distance between them is >>>
![D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/bn18956xdzpj56va064oiuu2531qoyd8xa.png)
The points given are (Sqrt(20), Sqrt(50)) and (Sqrt(125), Sqrt(8)), so their distance is >>>
![\begin{gathered} D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ D=\sqrt[]{(\sqrt[]{8}-\sqrt[]{50})^2+(\sqrt[]{125}-\sqrt[]{20})^2} \\ D=\sqrt[]{(\sqrt8)^2-2(\sqrt[]{8})(\sqrt[]{50})+(\sqrt[]{50})^2^{}+(\sqrt[]{125})^2-2(\sqrt[]{125})(\sqrt[]{20})+(\sqrt[]{20})^2} \\ D=\sqrt[]{8-2(2\sqrt[]{2})(5\sqrt[]{2})+50+125-2(5\sqrt[]{5})(2\sqrt[]{5})+20} \\ D=\sqrt[]{8-40+50+125-100+20} \\ D=\sqrt[]{63} \\ D=3\sqrt[]{7} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/utxecsl4xtj8iivxip83jxsomru8qcjpve.png)
----------------------------------------------------------------------------------------------------------
The midpoint formula is >>>
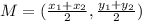
Plugging in the points, we have >>>
![\begin{gathered} M=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ M=(\frac{\sqrt[]{20}+\sqrt[]{125}}{2},\frac{\sqrt[]{50}+\sqrt[]{8}}{2}) \\ M=(\frac{2\sqrt5+5\sqrt[]{5}}{2},\frac{5\sqrt[]{2}+2\sqrt[]{2}}{2}) \\ M=(\frac{7\sqrt[]{5}}{2},\frac{7\sqrt[]{2}}{2}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9nvsiilfi4z987ikrv7pk4g13zdq2n7gkv.png)