Question

Find the direction angle of the vector w=4i-8j. That is, find the angle between 0 and 360° that w makes with the positive x-axis (measuredcounterclockwise), when w is in standard position.Do not round any intermediate computations, and round your answer to the nearest whole number.

Answer 1

297 degrees

Step-by-step explanation:

Given the vector: w=4i-8j

The x-coordinate is positive while the y-coordinate is negative, this implies that w is in Quadrant IV.

First, we find α below:

`\alpha=\arctan |(y)/(x)|=\arctan |-(8)/(4)|=\arctan |(8)/(4)|=63.43\degree`

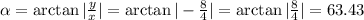
Next, we find the direction angle below:

`\begin{gathered} \text{For Quadrant IV: }\theta=360\degree-\alpha \\ =360\degree-63.43\degree \\ =296.57\degree \\ \approx297\degree \end{gathered}`

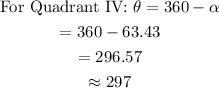
The angle that w makes with the positive x-axis (measured counterclockwise) is 297 degrees.