When two lines are parallel their slope is equal, when they're perpendicular the slopes are opposite reciprocal from each other.
To solve the problem we need to look for the slope of each line. To do that we will rewrite the expressions on it's slope-intercept form. This is done by isolating the "y" variable on the left side. The second equation already is in this form, therefore:
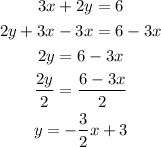
The slope of the line is the number multiplying "x" on the right side. The number on both lines is equal, this means that they are parallel.