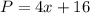Question

“Straight Ahead” isn’t part of the problem, that is just what this section of the problem is called.

Answer 1

To find the perimeter in terms of x, follow the steps below.

Step 01: Factor out the quadratic equation.

To do it, find its roots using the quadratic formula.

For a quadratic equation y = ax² + bx + c, the quadratic formula is:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this question:

a = 1

b = 8

c = 16

Then:

`\begin{gathered} x=\frac{-8\pm\sqrt[]{8^2-4\cdot1\cdot16}}{2\cdot1} \\ x=\frac{-8\pm\sqrt[]{64-64}}{2} \\ x=\frac{-8\pm\sqrt[]{0}}{2} \\ x_1=(-8-0)/(2)=-(8)/(2)=-4 \\ x_2=(-8+0)/(2)=-(8)/(2)=-4 \end{gathered}`

A quadratic equation in the factored form is y = (x - x₁)(x - x₂), where x₁ and x₂ are the roots.

Then, the quadratic equation can be written as:

`\begin{gathered} (x-(-4))\cdot(x-(-4)) \\ (x+4)\cdot(x+4) \end{gathered}`

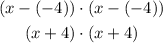
Step 02: Find the sides of the rectangle.

The area of the rectangle is:

`A=(x+4)\cdot(x+4)`

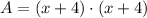
A rectangle with sides "a" and "b" has an area (A):

`A=a\cdot b`

Then, the sides of the triangle are:

a = x + 4

b = x + 4

Step 03: Find the perimeter.

A rectangle with sides "a" and "b" has the perimeter (P):

`P=2a+2b`

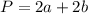
Since:

a = x + 4

b = x + 4

Then,

`P=2\cdot(x+4)+2\cdot(x+4)`

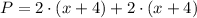
Solving the equation:

`\begin{gathered} P=2x+8+2x+8 \\ P=4x+16 \end{gathered}`

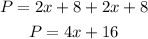
Answer:

The perimeter (P) is:

`P=4x+16`