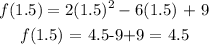Answer:
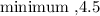
Step-by-step explanation:
Firstly, we need to know if we will have a maximum or a minimum
This is dependent on the value of the coefficient of x^2, if positive or negative
This value dictates the direction in which the graph will face. The value is positive here, and that means the parabola will open up. This makes the extreme point a minimum
Now,let us get its value
We start by finding the first differential of the function
That would give:
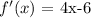
Now, we equate this to zero and get the value of x
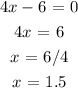
Finally, we go back to substitute this value into the equation
We have this as: