Answer:
The sample space is the set of elements in B i.e n(B) = 13
Step-by-step explanation:
The total number of cards in a deck of cards is 52
The number of cards that carry the number 10 is 4
The number of space cards is 13
The probability of the first event is thus 4/52 = 1/13
The probability of the second event is 13/52 = 1/4
Now, there is only a space card that carries the number 10
This means that the intersection of both events contains a single element in its sample space: n(A n B) = 1
We have the conditional probability as:
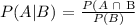
Substituting the values, we have it that:
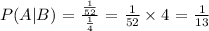
The denominator value 13 is the sample space for the conditional probability and that is the n(B) sample space3