Question

Determine how many real solutions tbe equation y=2x^2-4+10 has by using the discriminant

Answer 1

Consider the given quadratic equation,

`y=2x^2-4x+10`

Compare with the standard form,

`y=ax^2+bx+c`

It is obtained that,

`\begin{gathered} a=2 \\ b=-4 \\ c=10 \end{gathered}`

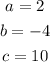
The discriminant is calculated as,

`\begin{gathered} D=b^2-4ac \\ D=(-4)^2-4(2)(10) \\ D=16-80 \\ D=-64 \end{gathered}`

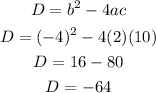
Since the value of the discriminant is less than zero, both the solutions of the given quadratic equation are imaginary.

Therefore, there is no real solutions of the quadratic equation.