Question

Find the perimeter and area of quadrilateral ZOID given Z1-6,5),(-8,3), I(14.-3),and D(-1,5).

Answer 1

We are asked to determine the perimeter and area of a quadrilateral given the coordinates of its vertices.

A diagram of the problem is the following:

First, we will find the perimeter, to do that we need to sum the length of all the sides of the quadrilateral. To determine the length of each side we will use the following formula for the distance between two points in a plane:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

We will find the distance between Z and O:

`\begin{gathered} d_(ZO)=\sqrt[]{(-6-(-8))^2+(5-3)^2} \\ d_(ZO)=\sqrt[]{2^2+2^2} \\ d_(ZO)=\sqrt[]{4+4}=\sqrt[]{8} \end{gathered}`

Now the distance between O and I:

`\begin{gathered} d_(OI)=\sqrt[]{(14-(-8))^2+(-3-3)^2} \\ d_(OI)=\sqrt[]{22^2+6^2} \\ d_(OI)=\sqrt[]{484+36} \\ d_(OI)=\sqrt[]{520} \end{gathered}`

Now the distance between I and D:

`\begin{gathered} d_(ID)=\sqrt[]{(-1-14)^2+(5-(-3))^2} \\ d_(ID)=\sqrt[]{15^2+8^2} \\ d_(ID)=\sqrt[]{225+64} \\ d_(ID)=\sqrt[]{289} \end{gathered}`

Now the distance between D and Z:

`\begin{gathered} d_(DZ)=\sqrt[]{(-6-(-1))^2+(5-5)^2} \\ d_(DZ)=\sqrt[]{5^2}=5 \end{gathered}`

Now the perimeter is the sum of each of the distances:

`P=d_(ZO)+d_(OI)+d_(ID)+d_(DZ)`

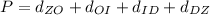
Replacing the values:

`P=\sqrt[]{8}+\sqrt[]{520}+\sqrt[]{289}+5`

Solving the operations

`P=520`

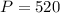
Therefore, the perimeter is 520.

Now we are asked to determine the area to do that we will use the following formula:

`A=(1)/(2)(x_1y_2+x_2y_3+x_3y_4+x_3y_4+x_4y_1)-(1)/(2)(x_2y_1+x_3y_2+x_4y_3+x_1y_4)`

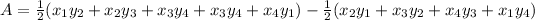
Replacing the values:

`A=(1)/(2)((-6)(3)+(-8)(-3)+(14)(5)+(-1)(5))+(1)/(2)((-8)(5)+(14)(3)+(-1)(-3)+(-6)(5))`

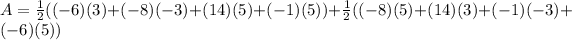
Solving the operation

`A=23`

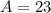
Therefore, the area is 23.