Question

I need the answer and work shown step by step

Answer 1

The equation of a circle is given by the formula:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ \text{where,} \\ \\ (a,b)=\text{ the coordinate of the center of the circle} \\ r=\text{radius of circle} \end{gathered}`

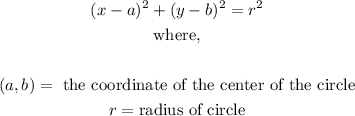
Now that we have the formula, we can compare the equation given in the question with the formula.

This way, we can easily make inferences as to what the coordinates of the center and radius are.

Let us proceed to compare them:

`\begin{gathered} (x-6)^2+(y-7)^2=169 \\ \text{compare this with:} \\ \\ (x-a)^2+(y-b)^2=r^2 \\ \\ \text{ We can s}ee\text{ that:} \\ (x-6)^2=(x-a)^2\text{ (find the square root of both sides to remove the squares)} \\ \sqrt[]{(x-6)^2}=\sqrt[]{(x-a)^2} \\ x-6=x-a \\ subtract\text{ x from both sides} \\ -6=-a\text{ ( divide both sides by -1)} \\ \therefore a=6. \\ \\ By\text{ the same logic:} \\ (y-b)^2=(y-7)^2 \\ y-b=y-7 \\ \\ \therefore b=7 \\ \\ \text{ Finally,} \\ r^2=169\text{ (find the square root of both sides to find the radius)} \\ \sqrt[]{r^2}=\sqrt[]{169} \\ \\ \therefore r=13 \end{gathered}`

Therefore, we can conlude that:

center: (6, 7), radius = 13 (Option A)