Question

Find the 22nd term of the arithmetic sequence whose common difference is d=4 and whose first term is (in the picture)

Answer 1

Hello there. To solve this question, we have to remember some properties about arithmetic sequences.

Given the first term of an arithmetic sequence and its common difference, we can determine the n-th term of the sequence using the following formula:

`a_n=a_1+(n-1)\cdot d`

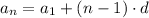
We know that a1 = 3 and d = 4, hence

`\begin{gathered} a_n=3+(n-1)\cdot4=3+4n-4 \\ \\ \Rightarrow a_n=4n-1 \end{gathered}`

Is the general formula for the n-th term of the sequence.

Plugging n = 22, we find

`a_(22)=4\cdot22-1=88-1=87`

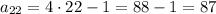
This is the 22nd term of this sequence.