Question

The Life of Trees ProjectPart A: Tree ResearchFive years ago your teacher planted a tree that was 24 inches tall and has tracked it's growth. You decided you want to plant a tree seed and see when both trees will be the same height.Teacher:Hickory (Shellbark)10'' per year80' when matureMe:White Ash18.5'' per year65' when maturePart B:Write a linear equation for each tree to represent it's growth each year. Fill in the following info to help.Identify your variables:x = time y = heightYour teacher planted his/her tree in year 0. Use point-slope formula to find your equation. Show your work.(supposed to be chart↓↓) Teacher Mepoint (y) 24 in (x) ←interceptsslopeequation(y = mx + b)I'm having trouble with the chart, I think the y-intercept (the one on the teacher's side of the chart) is 24'' cause the planted it when it was 24'' I'm just having trouble with the rest of it.

Answer 1

We can start by modeling the teacher's tree height.

First, we define as time x=0 as the time when the teacher plant the 24 inches tree.

Then, y(0) = 24. This is the y-intercept (b=24), as it is the value of y when x=0.

This tree grows 10 inches per year. This is the slope when y is expressed in inches and x is expressed in years. Then, m=10.

We can write the equation for the height of the teacher's tree as:

`\begin{gathered} y=mx+b \\ y=10x+24 \end{gathered}`

Our tree is planted at x=5 (five years after the teacher plant the tree) and, as it is planted from seed, the height at this time x=5 is y(5)=0.

The slope is equal to the growth rate, that is 18.5 inches a year. Then, m=18.5.

As we know one point of the line and the slope, we can write the equation in slope-point form and then re-arrange it into slop-intercept form:

`\begin{gathered} y-y_0=m(x-x_0) \\ y-0=18.5(x-5) \\ y=18.5x-18.5\cdot5 \\ y=18.5x-92.5 \end{gathered}`

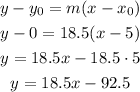
We then can find when the two trees reach the same height by equalizing both expressions for the heights:

`\begin{gathered} y_{\text{teacher}}=y_(me) \\ 10x+24=18.5x-92.5 \\ 24+92.5=18.5x-10x \\ 116.5=8.5x \\ x=(116.5)/(8.5) \\ x\approx13.7 \end{gathered}`

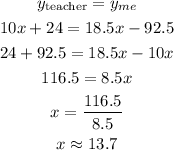
We can calculate the height of the trees when they have the same height by relacing x with 13.7 in anny of the 2 equations:

`y(13.7)=10(13.7)+24=137+24=161`

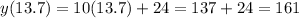
We can find the x-intercept by finding the values of x for y=0.

In our case, we know that at the moment of planting, x=5, the height is y=0, so the x-intercept is x=5.

In the case of the teacher, we have to calculate:

`\begin{gathered} y=0=10x+24 \\ 10x=-24 \\ x=-(24)/(10) \\ x=-2.4 \end{gathered}`

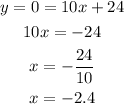
The x-intercept is x=-2.4.

We then can fill the table as:

Teacher:

Intercepts: x-intercept = -2.4, y-intercept = 24.

Slope: m = 10

Equation: y = 10x+24

Me:

Intercepts: x-intercept = 5, y-intercept = -92.5

Slope: m = 18.5

Equation: y=18.5x-92.5

Answer: the trees reach the same height, y=161 in., at time x=13.7 years.