Question

Determine if each pair of lines is parallel or not.

Answer 1

Two lines are parallel if their slopes are equal. The equation of a line in slope-intercept form, is:

`y=mx+b`

Where m is the slope of the line.

Write each equation in slope-intercept form to find if the slopes of each line are the same or not, which will tell us if they are parallel or not.

a)

First, isolate y from the first equation to write the equation in slope-intercept form:

`\begin{gathered} 2y=3x-5 \\ \Rightarrow y=(3)/(2)x-(5)/(2) \end{gathered}`

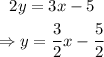
Notice that the slope of the first line is 3/2. Next, isolate y from the second equation:

`\begin{gathered} 8-y=-3x \\ \Rightarrow-y=-3x-8 \\ \Rightarrow y=3x+8 \end{gathered}`

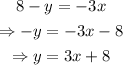
The slope of the second line is 3.

Therefore, this pair of lines is NOT parallel.

b)

Notice that both equations are already written in slope-intercept form:

`\begin{gathered} y=3 \\ y=-5 \end{gathered}`

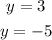
Since the variable x does not appear in the equation, this means that the coefficient of x is 0 in both cases. Then, the slope of these two lines is 0.

Therefore, this pair of lines IS parallel.