Question

37. Given: angle12 = angle 8, angle 8 = angle 4Prove: j || k and L||n

Answer 1

Given the figure below

It is given that angle 12 is congruent to angle 8, we are to prove that line j is parallel to line k

To achieve this, it can be seen that

`\begin{gathered} <12\cong<8(given) \\ <8\cong<2(alternate\text{ interior angle)} \end{gathered}`
`\sin ce<8\cong<2,then,<12\cong<2`

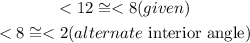
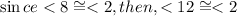
If line l is a transversal to line l is a transversal to line j and k, and given that tw lines are said to be parallel when a transversal cut them and the alternate exterior angles are equal

`<12\cong<2(alternate\text{ exterior angles, derived)}`

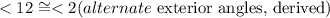
Since the transversal line 'l' cross line 'j' and 'k', and the alternate exterior angle are equal, hence, line j is parallel is line k

Given that angle 8 is congruent to angle 4, we would prove that line 'l' and line 'n' are parallel

To achieve this, it can be seen that

`\begin{gathered} <8\cong<4(given) \\ <4\cong<10(alternate\text{ interior angle)} \\ <10\cong<12(vertically\text{ opposite angle)} \\ <8\cong<12(alternate\text{ exterior angle, derived)} \end{gathered}`

If line j is transversa to line 'l' and line 'n' and given that two lines are said to be parallel when a transversal cut them and the alternate exterior angles are equal.

Since the transversal line 'j' cross line 'l' and 'n', and the alternate exterior angle are equal, hence, line 'l' is parallel is line 'n'