Question

put the Equations in slope-intercept form(a)and then identifying the equations as(b) parallel or perpendicular lines 1:Slope- intercept form for-2xty=7?2 slope -intercept form for y-5=2x?

Answer 1

Given

The equations are,

`\begin{gathered} 2x+y=7\text{ \_\_\_\_\_\_\_\_\lparen1\rparen} \\ y-5=2x\text{ \_\_\_\_\_\_\_\lparen2\rparen} \end{gathered}`

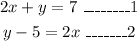
To find the slope intercept form and to check whether the lines are parallel or perpendicular.

Step-by-step explanation:

It is given that,

`\begin{gathered} 2x+y=7\text{ \_\_\_\_\_\_\_\_\lparen1\rparen} \\ y-5=2x\text{ \_\_\_\_\_\_\_\lparen2\rparen} \end{gathered}`

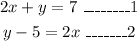
Since the slope intercept form is defined as,

`\begin{gathered} y=mx+c \\ where,\text{ }m\text{ }is\text{ }the\text{ }slope. \end{gathered}`

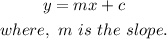
Then, (1) can be written as,

`\begin{gathered} y=-2x+7 \\ Here,\text{ }m_1=-2.\text{ \_\_\_\_\lparen3\rparen} \end{gathered}`

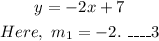
And, (2) can be written as,

`\begin{gathered} y=2x+5 \\ Here,\text{ }m_2=2.\text{ \_\_\_\_\lparen4\rparen} \end{gathered}`

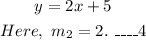
From (3) and (4),

`\begin{gathered} m_1\\e m_2 \\ m_1* m_2\\e-1 \end{gathered}`

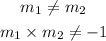
Hence, the equations are neither parallel nor perpendicular.