Question

part A: a data set is normally distributed with a mean of 27 and a standard Deviation of 3.5. find the Z score for a value of 25 to the nearest hundredth.part B: from part A about what percentage of the data is greater then 34?48%2%4%0.2%

Answer 1

Let x=25, μ=27, and σ=3.5.

To obtain the z-score, substitute the given values into the following equation and then simplify the expression.

`\begin{gathered} z=(x-\mu)/(\sigma) \\ z=(25-27)/(3.5) \\ z=-(2)/(3.5) \\ z\approx-0.57 \end{gathered}`

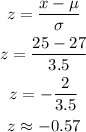
The 34 is 2 standard deviations away from the mean. This means we added 2σ=2(3.5)=7 to the mean which is 27.

Thus, using the 68-95-99 rule, we know that the percentage above the μ+2σ is about 2.5%. Thus, from the choices, the answer is 2%.