Question

In the figure below, QS is the angle bisector of

Answer 1

We need to find the value of x.

We know that QS is the angle bisector of ∠PSR. Thus, we have:

`\angle PSQ=\angle RSQ`

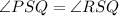
Also, both triangles have a right angle. Then, the two triangles formed are similar because they have two congruent corresponding angles.

Also, they share side QS. Thus, the proportion factor between the corresponding sides is 1, i.e., the corresponding sides are congruent.

Therefore, the two triangles are congruent, and we have:

`\begin{gathered} 8x-27=4x+33 \\ \\ 8x-27-4x=4x+33-4x \\ \\ 4x-27=33 \\ \\ 4x-27+27=33+27 \\ \\ 4x=60 \\ \\ (4x)/(4)=(60)/(4) \\ \\ x=15 \end{gathered}`

Answer: x = 15