We are given 2 statements.
We translate them to algebraic statements.
Let
smaller integer be s, and
larger integer be l
"The larger of two integers is 4 more than 9 times the smaller."
We can write this as:
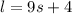
Then, we are given sum of 2 integers is greater than or equal to 26, we can write:

We put 1st equation in 2nd:

The next integer value (smallest of them all) of s is "3".
Now, if s is 3, l would be:
l = 9s + 4
l = 9(3) + 4
l = 27 + 4
l = 31
smaller of the both integers:
Smaller Number: 3
Larger Number: 31