24.28 units
Step-by-step explanationPerimeter is the distance around the edge of a shape, to find the perimeter of the given figure we can use the distance bewteen 2 points formula,it says
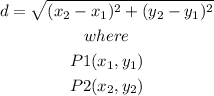
so
Step 1
identify the vertices ;
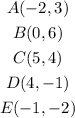
Step 2
now, find the length of each segment
a)AB
replace in the formula
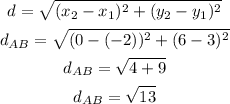
b)BC
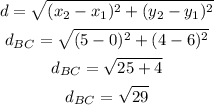
c)CD
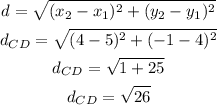
d)DE
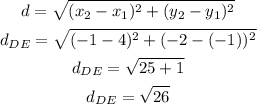
e) EA
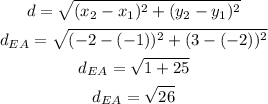
Step 3
finally, the perimeter is the sum of the sides length, so
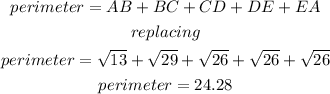
so, the perimeter is 24.28 units