Question

Find the interest rate for a $2000 deposit accumulating to $2682, compounded annually for six years.The interest rate is ??%

Answer 1

We are asked to determine the interest rate for a deposit compounded annually. To do that we will use the following formula:

`A=P(1+r)^t`

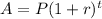
Where "r" is the interest rate, "A" is the accumulated quantity, "P" the initial deposit and "t" is time. We will solve for "r" first by dividing both sides by "P":

`(A)/(P)=(1+r)^t`

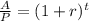
Now we will take root on both sides:

`\sqrt[t]{(A)/(P)}=1+r`

Now we subtract 1 to both sides:

`\sqrt[t]{(A)/(P)}-1=r`

Now we replace the values:

`\sqrt[6]{(2682)/(2000)}-1=r`

Solving the operations:

`\sqrt[6]{1.341}-1=r`
`\begin{gathered} 1.05-1=r \\ 0.05=r \end{gathered}`

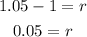
Therefore, the interest rate is 5%.