Question

A triangular prism is attached to a rectangular prism as shown below.If W= 6 1/5th inches, x= 5 inches, y= 20 inches, and z=8 3/4th inches, what is the surface area of the figure

Answer 1

To answer that question we can find the surface area of the triangular prism, the surface area of the parallelogram, and after, remove the area where the parallelogram has contact with the triangular prism

`\begin{gathered} A_S=A_(prism)+A_(parallelogram) \\ \\ A_(prism)=(w^2)/(2)\cdot2+2\cdot wy+zy \\ \\ A_(parallelogram)=2x^2+4\cdot xy \end{gathered}`

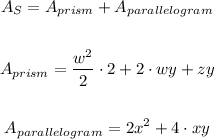
Therefore, we can simplify it to

`A_(prism)=w^2+wy+zy`

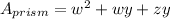
And the parallelogram

`A_(parallelogram)=2x^2+4xy`

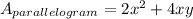
See that one face of the parallelogram has a contact with the prism, it's the area that we must subctract, it's xy, therefore

`\begin{gathered} A_S=w^2+wy+zy+2x^2+4xy-xy \\ \\ A_S=w^2+wy+zy+2x^2+3xy \end{gathered}`

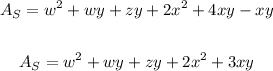
The formula to find the surface area of the figure is

`A_S=w^2+wy+zy+2x^2+3xy`

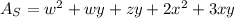
Remember that

`\begin{gathered} w=6.2 \\ x=5 \\ y=20 \\ z=8.75 \end{gathered}`

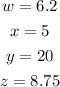
Therefore

`\begin{gathered} A_S=6.2^2+6.2\cdot20+8.75\cdot20+2\cdot5^2+3\cdot5\cdot20 \\ \end{gathered}`

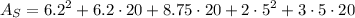
Put it in a calculator

`A_S=687.44\text{ }\imaginaryI\text{nches}^2`