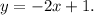Step-by-step explanation
The slope-intercept equation of a line has the form

where m is the slope of the line and b is its y-intercept.
Now, there is a very interesting relationship between the slopes (m_1 and m_2) of perpendicular lines:
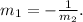
Looking at the given equation, we can say that its slope is 1/2. Then,
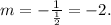
Then, our desired equation becomes
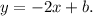
Now, we know that our line passes through (-2,5). This means that
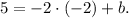
Solving this equation for b, we get
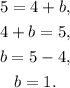 Answer
AnswerThe desired line has equation