Question

An arrow is shot vertically upward at a rate of 210 feet per second from ground level. Use the projectile formula h = -16t^2 + Vv0t + hv0to determine when the height of the arrow will be 166 feet.

Answer 1

First, lets see what info we have. The proyectile formula is:

`\begin{gathered} h=-16t^2+v_0t+h_0 \\ \end{gathered}`

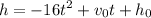
Where v0 is the initial velocity and h0 is the initial speed.

The initial speed is 210ft per second, and since the arrow is shot from ground level, h0 = ft

Thus, the proyectile formula is:

`h=-16t^2+210t`

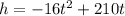
And now we want to find the time the arrow is at 166 ft. This means we want h = 166ft

We write:

`\begin{gathered} 166=-16t^2+210t \\ 0=-16t^2+210t-166 \end{gathered}`

And now we can use the quadratic equation. For a quadratic equation of the form:

`0=ax^2+bx+c`

The solutions are:

`x_(1,2)=(-b\pm√(b^2-4ac))/(2a)`

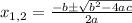
In this case:

a = -16

b = 210

c = -166

We write:

`\begin{gathered} x_(12)=(-210\pm√(210^2-4\cdot(-16)\cdot(-166)))/(2\cdot(-16))=(-210\pm√(44100-10624))/(-32)=(210\pm182.96)/(32) \\ x_1=(210+182.96)/(32)=12.28 \\ x_2=(210-182.96)/(32)=0.84 \end{gathered}`

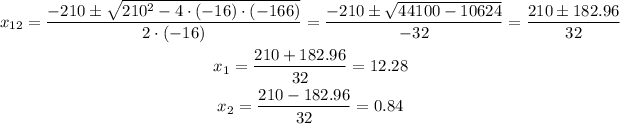
Thus the arrow goes up to 166ft after 0.84 seconds, and then once again (in it's path down) at 12.28 seconds