Question

Nothing changes with tangent

Answer 1

hello

to solve this question, we have to use trigonometric ratios and in this case, it was specified to use tangent

from the image above, we can see that we have the value of angle and opposite and we need to look for adjacent

trigonometric ratio is given as SOH CAH TOA

`\begin{gathered} \text{soh}=\text{sin}\theta=\frac{opposite}{\text{hypothenus}} \\ \text{cah}=\cos \theta=(adjacent)/(hypothenus) \\ \text{toa}=\tan \theta=(opposite)/(adjacent) \end{gathered}`

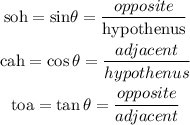
now, let's use the formula of tangent to solve this problem

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \text{opposite}=42 \\ \theta=64^0 \\ \text{adjacent}=x \\ \tan 64=(42)/(x) \\ x=(42)/(\tan 64) \\ x=20.48 \end{gathered}`

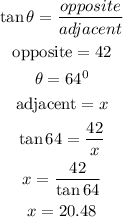
from the calculations above, the value of x is equal to 20.48