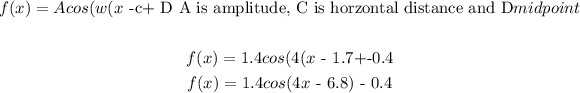Question

Given the graph below write an equation of the form f(x) = Acos(w(x-c))+D

Answer 1

Amplitude = (Maximum + Minimum)/2 , = (1 + 1.8)/2= (2.8)/2= 1.4

Period = distance for the function to repeat. So, the distance is from -0.5 to 3.5, then it is 4, then it is smaller than 2 times pi number.

C is the distance from the Y axis to the function.

D is the horizontal line that passes through the middle of the distance between the maximum and minimum point, which is in that case the same one as the period has to use

Then, the formula is:

`\begin{gathered} f(x)=Acos(w(x\text{ -c\rparen + D A is amplitude, C is horzontal distance and D}midpoint \\ \\ f(x)=1.4cos(4(x\text{ - 1.7\rparen+\lparen-0.4\rparen} \\ f(x)=1.4cos(4x\text{ - }6.8)\text{ - }0.4 \end{gathered}`