Solventar for g (2)/(5) (5g - 10) \geqslant 10

Question

Solventar for g
`(2)/(5) (5g - 10) \geqslant 10`

Answer 1

We can see the next inequality:

`(2)/(5)(5g-10)\ge10`

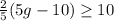
And we need to solve the inequality for g.

1. To find the values for g, we have to apply some properties. Then we can start by multiplying both sides by 5/2 as follows:

`\begin{gathered} (5)/(2)((2)/(5)(5g-10))\geqslant(5)/(2)(10) \\ \\ (5)/(5)(2)/(2)(5g-10)\ge5((10)/(2))\rightarrow(a)/(a)=1,(5)/(5)=1,(2)/(2)=1 \\ \\ 5g-10\ge5(5) \\ \\ 5g-10\ge25 \end{gathered}`

2. Now, we have to add 10 to both sides of the inequality as follows:

`\begin{gathered} 5g-10+10\ge25+10 \\ \\ 5g\ge35 \end{gathered}`

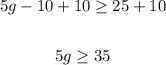
3. Finally, we have to divide both sides of the inequality by 5:

`\begin{gathered} (5g)/(5)\ge(35)/(5) \\ \\ g\ge7 \end{gathered}`

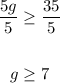
Therefore, in summary, the solutions for g are given by values equal to or greater than 7, and we can express it as inequality or as an interval notation:

`\begin{gathered} g\ge7 \\ \\ \text{ \lbrack7,}\infty) \end{gathered}`

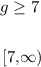
And this can be seen on the number line as follows: