Question

the previous expression equals 0 by which of the following ? a)sum identity for cosine b) difference identity for sine c) difference identity for cosine d)sum identity for sine e) no identity is required. the previous expression simplifies to the right side of the identity

Answer 1

The given expression is

`\cos ((7\pi)/(4)+x)+\sin ((5\pi)/(4)+x)=0`

Let's apply the sum identity to each one

`\begin{gathered} \cos ((7\pi)/(4)+x)=\cos ((7\pi)/(4))\cos (x)-\sin ((7\pi)/(4))\sin (x) \\ \sin ((5\pi)/(4)+x)=\sin ((5\pi)/(4))\cos (x)+\cos ((5\pi)/(4))\sin (x) \end{gathered}`

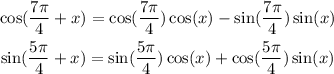
Then, we replace these expressions

`\begin{gathered} \cos ((7\pi)/(4))\cos (x)-\sin ((7\pi)/(4))\sin (x)+\sin ((5\pi)/(4))\cos (x)+\cos ((5\pi)/(4))\sin (x)=0 \\ \end{gathered}`

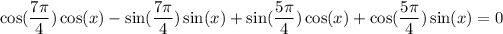
Now, we evaluate the expressions where x = 90°. Also, we know that pi = 180°.

`\cos ((7\cdot180)/(4))\cos (90)-\sin ((7\cdot180)/(4))\sin (90)+\sin ((5\cdot180)/(4))\cos (90)+\cos ((5\cdot180)/(4))\sin (90)=0`

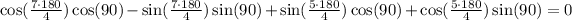
If we solve and simplify, we get

`-\sin (315)+\cos (315)=0`

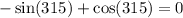
But, sin(315) = cos(315), so their difference is zero.

Hence,

`0=0`

The identity is proven.

Hence, the identity required was the sum identity for sine and cosine.