Question

the numberof blocks has 9 in the ones places.The number in the hundreds place is one more than the number in the tens place. Those two numbers equal 11. How many blocks are there?

Answer 1

Based on the given information, we can express the following

`\begin{gathered} h=1+t \\ h+t=11 \end{gathered}`

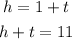
Because the digit of hundreds is 1 more the tens, and they sum 11. Let's combine the function to find t

`\begin{gathered} h+t=11 \\ 1+t+t=11 \\ 2t=11-1 \\ t=(10)/(2)=5 \end{gathered}`

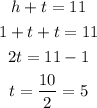
So, the digit of tens is 5.

Let's find the hundreds.

`h=1+t=1+5=6`

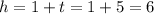
The number of hundreds is 6.

Hence, the number of blocks is 659.