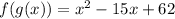Given
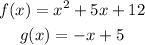
You have to calculate f(g(x))
You have to calculate the composite of the functions, this means, replace g(x) into f(x)
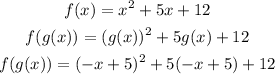
Once you replaced g(x) into f(x) you can solve the polynomial
The first step is to solve the terms in parentheses, to make it easier I'll solve them separatelly and then put the results together.
1) To solve the binomial square, you have to apply the distributive property of multiplications

2) To solve the multiplication of the parentheses term by multiplying each term by 5

Now put the results together and order the like terms together
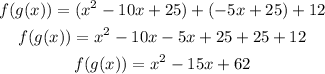
The result of the combination is