SOLUTION
Consider the image below
The ratio of the side is given by

Since the ratio of the side is the scale factor
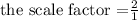
hence The raio of the perimeters is the scale factor
Therefore
The ratio of their parimeter is 2 : 1
The ratio of the Areas is square of the scale factor
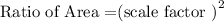
Hence

Therefore
The ratio of their Areas is 4 :1