Question

The function h (t) = -4.9t² + 19t + 1.5 describes the height in meters of a basketball t secondsafter it has been thrown vertically into the air. What is the maximum height of the basketball?Round your answer to the nearest tenth.1.9 metersO 19.9 meters16.9 metersO 1.5 meters

Answer 1

Since the function describing the height is a quadratic function with negative leading coefficient this means that this is a parabola that opens down. This also means that the maximum height will be given as the y component of the vertex of the parabola, then if we want to find the maximum height, we need to write the function in vertex form so let's do that:

`\begin{gathered} h(t)=-4.9t^2+19t+1.5 \\ =-4.9(t^2+(19)/(4.9)t)+1.5 \\ =-4.9(t^2+(19)/(4.9)t+((19)/(9.8))^2)+1.5+4.9((19)/(9.8))^2 \\ =-4.9(t+(19)/(9.8))^2+19.9 \end{gathered}`

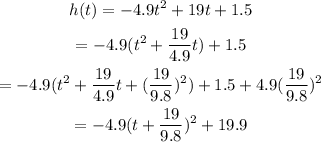
Hence the function can be written as:

`h(t)=-4.9(t+1.9)^2+19.9`

and its vertex is at (1.9,19.9) which means that the maximum height of the ball is 19.9 m