Question

For the polynomial below, 1 is a zero.h(x) = x² – 3x? - 2x + 4Express h(x) as a product of linear factors.

Answer 1

Step 1

Given the zero, 1, we can use synthetic division to acquire the other factors

Using synthetic division we will write out all coefficients of the terms of h(x) and proceed thus

1 | 1 -3 -2 +4

1 -2 -4

-----------------------

1 -2 -4 0

Hence the quadratic equation we will need to split into linear factors is given as

`x^2-2x-4`

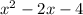
Since the remainder is 0

Step 2

Factorize the quadratic equation above completely

`\begin{gathered} x^2-2x-4=0 \\ we\text{ will use} \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

Where

a= 1

b= -2

c= -4

`\begin{gathered} x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4*1*-4}}{2*1} \\ x=\frac{2\pm\sqrt[]{4+16}}{2} \end{gathered}`
`\begin{gathered} x=\frac{2\pm\sqrt[]{20}}{2} \\ x=(2)/(2)+\frac{\sqrt[]{20}}{2}=1+\frac{2\sqrt[]{5}}{2}=1+\sqrt[]{5} \\ Or \\ x=(2)/(2)-\frac{\sqrt[]{20}}{2}=1-\frac{2\sqrt[]{5}}{2}=1-\sqrt[]{5} \end{gathered}`

Hence the product of linear factor will be

`(x-1)(1+\sqrt[]{5})(1-\sqrt[]{5})`