Calculate the derivative of the function, as shown below
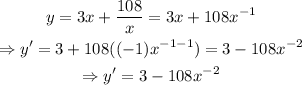
Set y'=0 and solve for x, as shown below
![\begin{gathered} y^(\prime)=0 \\ \Rightarrow3-108x^(-2)=0,x\\e0 \\ \Rightarrow3=(108)/(x^2) \\ \Rightarrow x^2=(108)/(3) \\ \Rightarrow x^2=36 \\ \Rightarrow x=\pm\sqrt[]{36} \\ \Rightarrow x=\pm6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q5nu5hd6pp7h3y7z52aizvqcw2i905v2da.png)
Their corresponding y-coordinates are
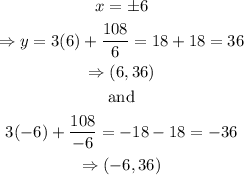
Therefore, the two stationary points are (6,36) and (-6,-36).
Using the second derivative test,
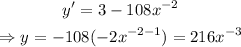
Then,
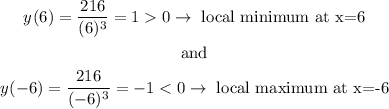
(6,36) is a local minimum and (-6,-36) is a local maximum.